11.3 Area calculation
Completion requirements
In this Book module, you will be going to learn about the calculation of the area using the grid method and the direct method.
Read and watch the different resorce in this book completly.
2. Area by direct method
1. Area of the square and rectangle.
2. Area of different shapes
Here is an example of the surface area using a square:
This square is 4 units long on each side. The surface area is the number of square units that fit into the square. As shown in the picture, the surface area of this square is 16 total square units.
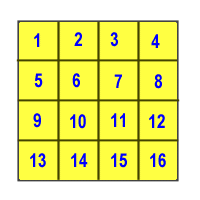
Area = W x L
Area = 4 x 4
Area = 16
Hey, that's the same answer!
Note: if the units were feet for this problem, the answer would be 16 feet squared. Not just 16 feet. When we give the answer for surface area we used squared to indicate that it's a surface area and not just a straight line.
Let's take the more complicated example of this football field. We used this same example to demonstrate how to figure the perimeter . The perimeter of this football field is the sum of all the sides 100 + 50 + 100 + 50 = 300 yards.
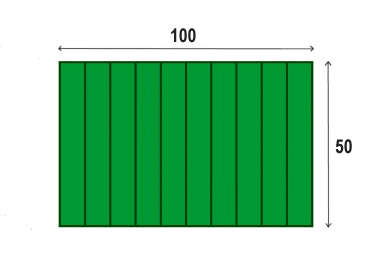
What is the surface area using yards for the units? Since this is a rectangle we can use the rectangle formula:
Area = W x L
Area = 100 yards x 50 yards
Area = 5000 yards squared